Nits, Lux, Lumen, Candela - mit Licht und Beleuchtung rechnen

Wenn im Sommer die Sonne zur Mittagszeit im Zenit steht, dann sind das ca. 90000 Lux. Die neue Lampe für das Badezimmer soll 400 Lumen hell sein. Eine Kerze hat eine Helligkeit von 1 Candela, und das Display eines Notebooks wird mit 300 Nits beschrieben.
Das sind alles Angaben, die etwas mit Helligkeit zu tun haben, aber jedes dieser Beispiele nutzt andere Einheiten. Wie hängen die zusammen? Tatsächlich handelt es sich hier meist um offizielle physikalische Einheiten und nicht um irreführendes Marketing - nur werden jeweils leicht unterschiedliche Aspekte von Licht und Beleuchtung beschrieben. Wenn bekannt ist, welche Einheit für welche physikalische Eigenschaft steht, dann lässt sich der Himmel im Sommer auch mit der Lampe und dem Display vergleichen.
Strahlungsleistung
Beginnen wir mit der Strahlungsleistung. Wie auch bei der mechanischen Leistung beschreibt die Strahlungsleistung eine Energiemenge pro Zeiteinheit. Bei der Strahlungsleistung wird diese Energie in Form von elektromagnetischen Wellen transportiert. Und ebenfalls genau wie bei der mechanischen Leistung ist die Einheit der Strahlungsleistung das Watt.

Der Begriff Strahlungsleistung wird für sämtliche elektromagnetischen Wellen verwendet, nicht nur für sichtbares Licht. Die Angabe in (Milli-)Watt findet sich z.B. auch bei WLAN-Routern, die in praktisch allen Ländern eine Obergrenze der Strahlungsleistung haben, die sie nicht überschreiten dürfen.
Das einzig Besondere am sichtbaren Licht ist die Tatsache, dass unsere Augen es wahrnehmen können (und das hat sich evolutionär so entwickelt, weil unser Stern in diesem Wellenlängenbereich seine höchste Strahlungsleistung hat).
Wir Menschen sehen jedoch auch im Bereich des sichtbaren Lichts, also bei Wellenlängen zwischen ca. 400 nm und 780 nm, nicht die Strahlung an sich, sondern nehmen sie je nach Wellenlänge unterschiedlich genau wahr. Das liegt daran, dass wir für diese Wellenlängen jeweils verschiedene Zapfen und Stäbe in unserer Netzhaut haben, die in Abhängigkeit von der jeweiligen Wellenlänge unterschiedlich gut darin sind, diese Strahlung verarbeiten.
Weil uns ja nun meist interessiert, was wir tatsächlich sehen können, und weniger, was an sich ausgestrahlt wird, unterscheidet die Physik zwischen radiometrischen Eigenschaften, die die Strahlung an sich beschreiben, und photometrischen Eigenschaften, die beschreiben sollen, was wir wahrnehmen können.
Lichtstrom
Zusätzlich zur radiometrischen Strahlungsleistung wurde deshalb ein photometrisches Gegenstück eingeführt: der Lichtstrom.
Der Lichtstrom beschreibt die Strahlungsleistung im Verhältnis zur Sensitivität des menschlichen Auges. Weil diese Sensitivität wellenlängenabhängig ist, wurde für die Definition die Empfindlichkeit bei 555 nm (der Farbe Grün) als Referenz festgelegt, weil diese Wellenlänge dem sensitivsten Punkt auf der Helligkeitsempfindlichkeitskurve entspricht.
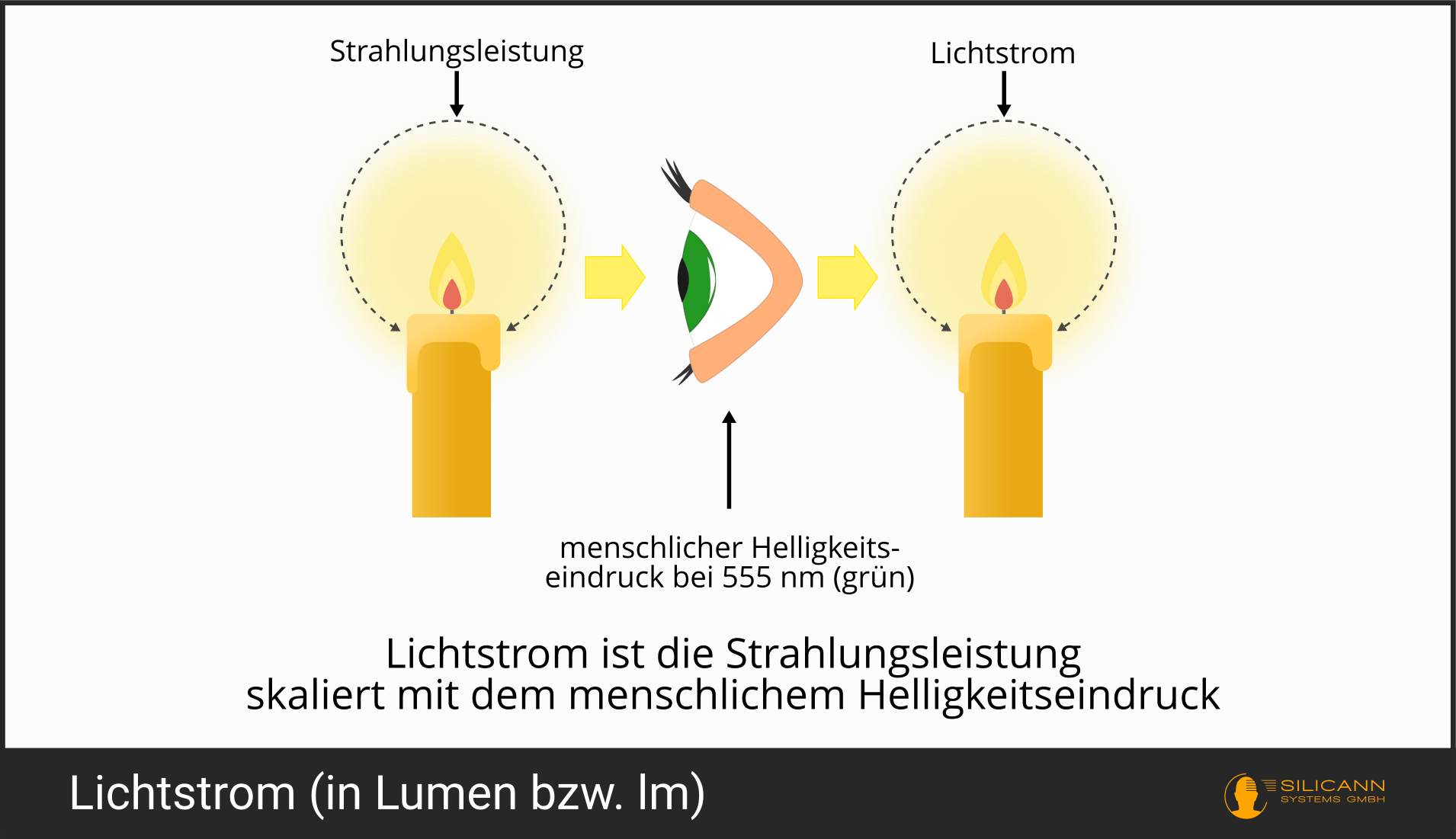
Diese photometrische Betrachtung würde rein rechnerisch nichts an der Einheit Watt ändern: Die Sensitivität bei jeder Wellenlänge wäre ja nur ein Faktor, eine Zahl ohne Einheit, so dass am Ende wieder das Watt als Einheit stehen würde. Damit aus der Einheit jedoch eindeutig hervorgeht, ob es sich um die radiometrische Strahlungsleistung oder den photometrischen Lichtstrom handelt, wurde für den Lichtstrom eine neue Einheit eingeführt: das Lumen.
Bei einer Wellenlänge von 555 nm beträgt das Umrechnungsverhältnis 683 lm/W. Da wir bei anderen Wellenlängen bei gleicher Strahlungsleistung weniger wahrnehmen ist in diesen Fällen der Skalierungsfaktor geringer.
Wird der Wert nicht weiter spezifiziert, und das ist in der Praxis meist der Fall, dann handelt es sich um unser Helligkeitsempfinden beim Tagsehen. Das Tagsehen ist bestimmt durch die Zapfen in unserer Netzhaut, die wir auch für die Farbwahrnehmung nutzen. Die Stäbchen dagegen werden nur für das Nachtsehen verwendet. Weil wir von ihnen nur eine Form haben und nicht drei wie bei den Zapfen, können wir mit ihrer Hilfe auch die Wellenlängen nicht unterscheiden - deshalb erscheinen uns nachts alle Katzen so grau. Dafür sind die Stäbchen aber deutlich empfindlicher: Beim Nachtsehen und der sensitivsten Wellenlänge, 507 nm, entspricht 1 Watt Strahlungsleistung einem Lichtstrom von 1700 lm.
Lichtstärke
Der Lichtstrom beschreibt das sichtbare Licht, das von der Lichtquelle insgesamt ausgestrahlt wird. Manchmal interessiert uns aber nur das Licht innerhalb eines bestimmten Raumwinkels, nicht das gesamte Licht. Ein Beispiel wäre Straßenbeleuchtung: Ziel ist ja eine erleuchtete Straße, nicht der erleuchtete Himmel. Von Interesse ist also nur der Teil des Lichtstroms, der in Richtung Straße ausgestrahlt wird. Dieses Verhältnis von Lichtstrom und Raumwinkel ist die Lichtstärke.
So wie ein Winkel den Ausschnitt eines Kreises beschreibt, ist der Raumwinkel ein Ausschnitt einer Kugel. Die Einheit des Raumwinkels heißt Steradiant, abgekürzt sr. Wenn wir eine Kugel mit einem Radius von einem Meter betrachten, dann beschreibt ein Raumwinkel von 1 sr einen Kreisausschnitt, dessen Fläche genau 1 m² groß ist. Eine volle Kugel hätte einen Raumausschnitt von 4π sr.
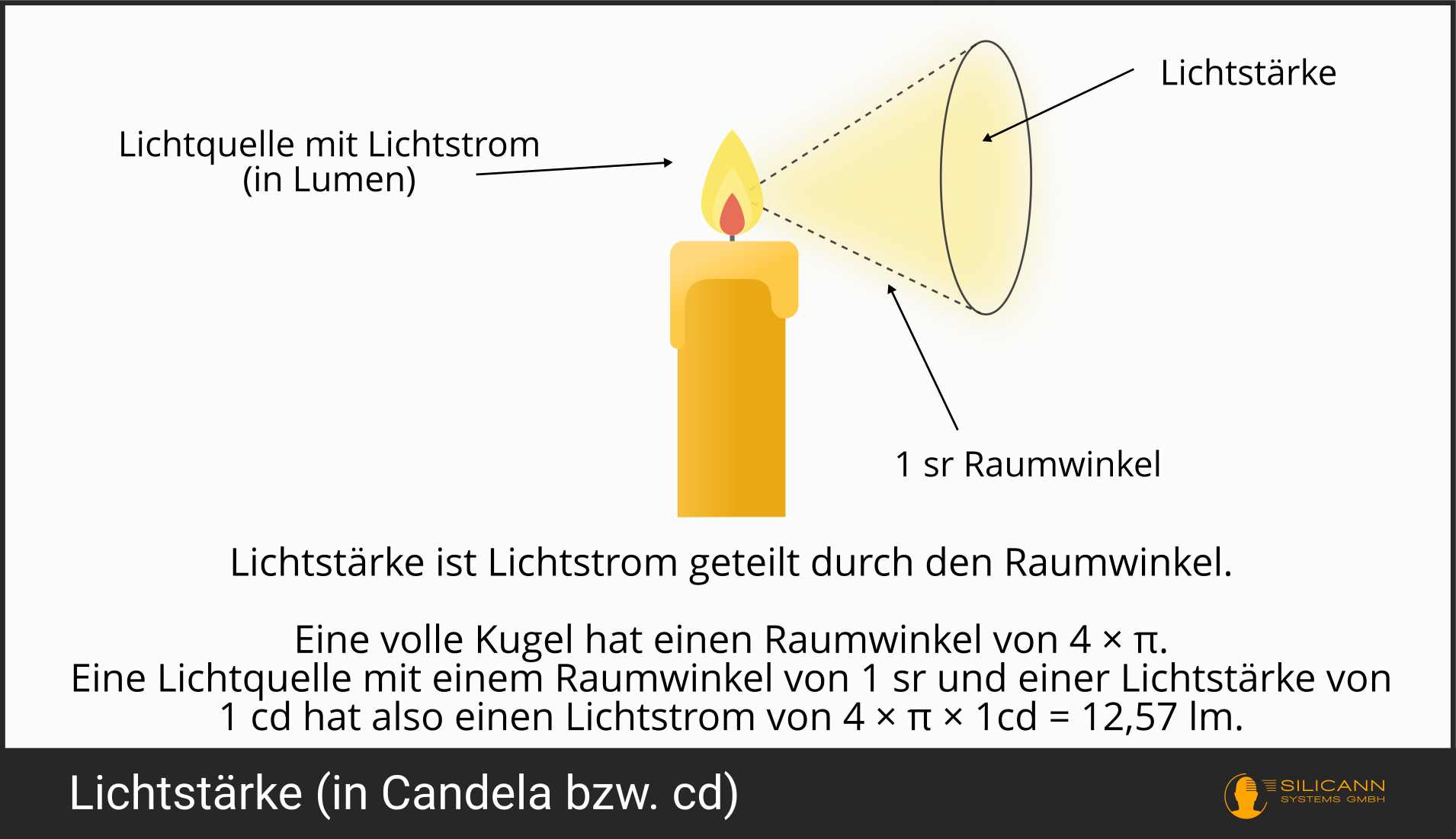
Die Lichtstärke wird in Candela bzw. kurz cd angegeben. Candela ist das lateinische Wort für Kerze, und tatsächlich orientierte sich diese Einheit ursprünglich an echten Kerzen: Ein Candela sollte ungefähr der Lichtstärke einer Kerze entsprechen.
Candela ist definiert als das Verhältnis von Lichtstrom und Raumwinkel, also lm/sr.
Eine echte Kerze strahlt ihr Licht ja praktisch vollständig kugelförmig aus. Wenn ihre Lichtstärke also 1 cd beträgt, dann können wir ihren Lichtstrom ausrechnen: Lichtstrom = Lichtstärke × 4 × π = 12,57 lm.
Spezifische Lichtausstrahlung
Nicht jede Lichtquelle lässt sich aber so punktförmig beschreiben wie eine Kerze oder eine Lampe aus einem Meter oder mehr Abstand. Manche Lichtquellen müssen aufgrund ihrer besonderen Anwendung als Fläche behandelt werden, die gleichmäßig über ihre gesamte Ausbreitung ausstrahlt. Zum Beispiel wird die Oberfläche von SMD-LEDs häufig auf diese Weise betrachtet, als Fläche, die aus lauter kleinen Punktlichtquellen besteht, deren Ausstrahlungswinkel sich jeweils so überschneiden, dass die gesamte Oberfläche ein einheitlich strahlendes Element bildet.
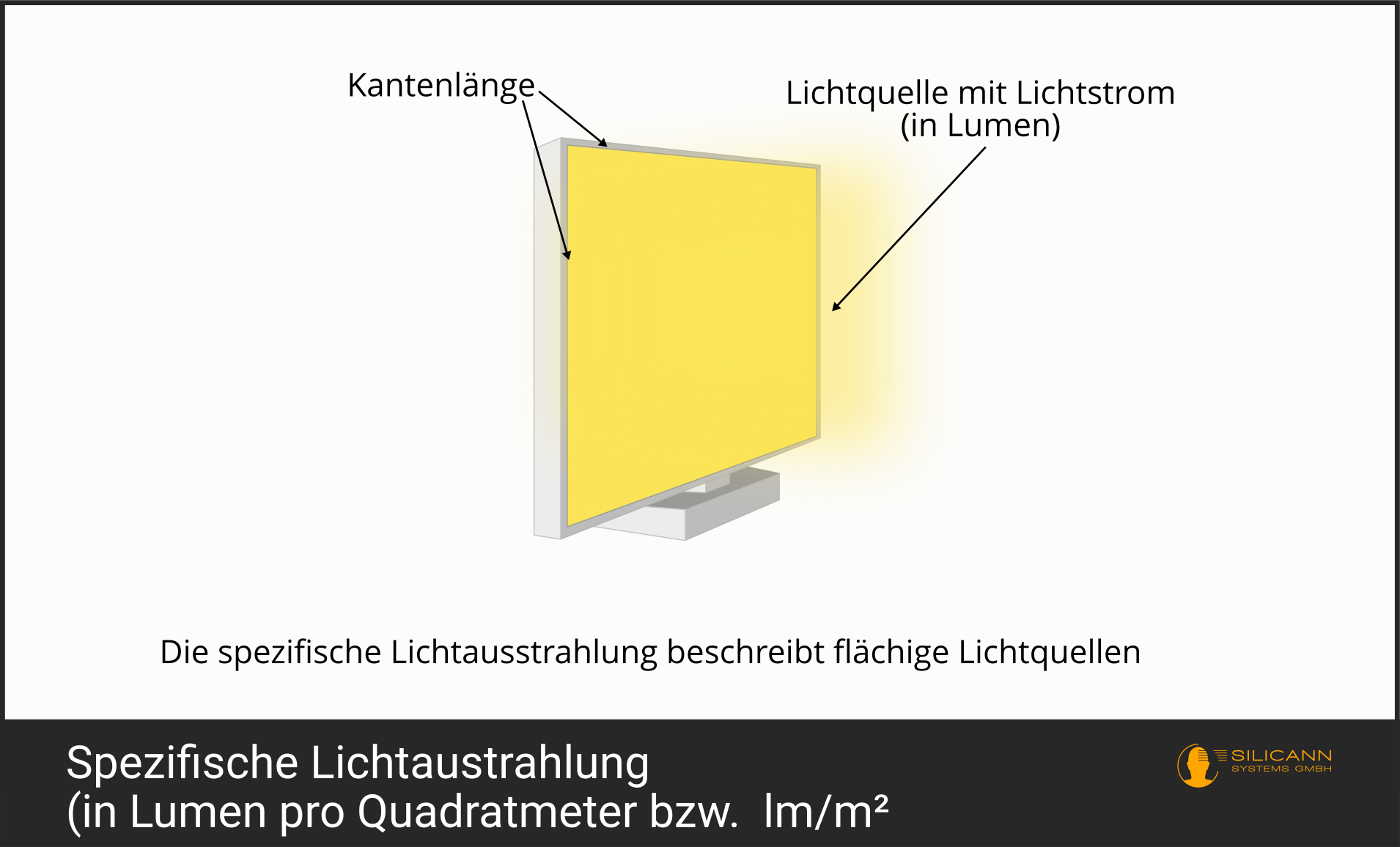
Die spezifische Lichtausstrahlung solcher Flächenstrahler wird dann mit lm/m² angegeben: Der von ihr ausgehende Lichtstrom (angegeben in Lumen) steht im Verhältnis zur strahlenden Fläche (in m²).
Warum gibt es überhaupt diese Unterscheidung zwischen Lichtstrom und spezifischer Lichtausstrahlung, d.h. warum wird der Helligkeitseindruck nicht einfach nur in Lumen angegeben? Weil unser Sehsystem eine Lichtquelle als heller einstuft, wenn sie denselben Lichtstrom über eine kleinere Fläche ausstrahlt.
Die ausstrahlende Fläche findet bei der spezifischen Lichtausstrahlung also Berücksichtigung. Der Ausstrahlungswinkel des Strahlers wird in diesem Fall jedoch nicht betrachtet.
Leuchtdichte
So kann man aber nicht mit jeder Lichtquelle verfahren - in vielen Fällen spielt der Winkel nämlich eine große Rolle für den Helligkeitseindruck, der sich für die betrachtende Person ergibt. Das trifft beispielsweise auf Displays zu.
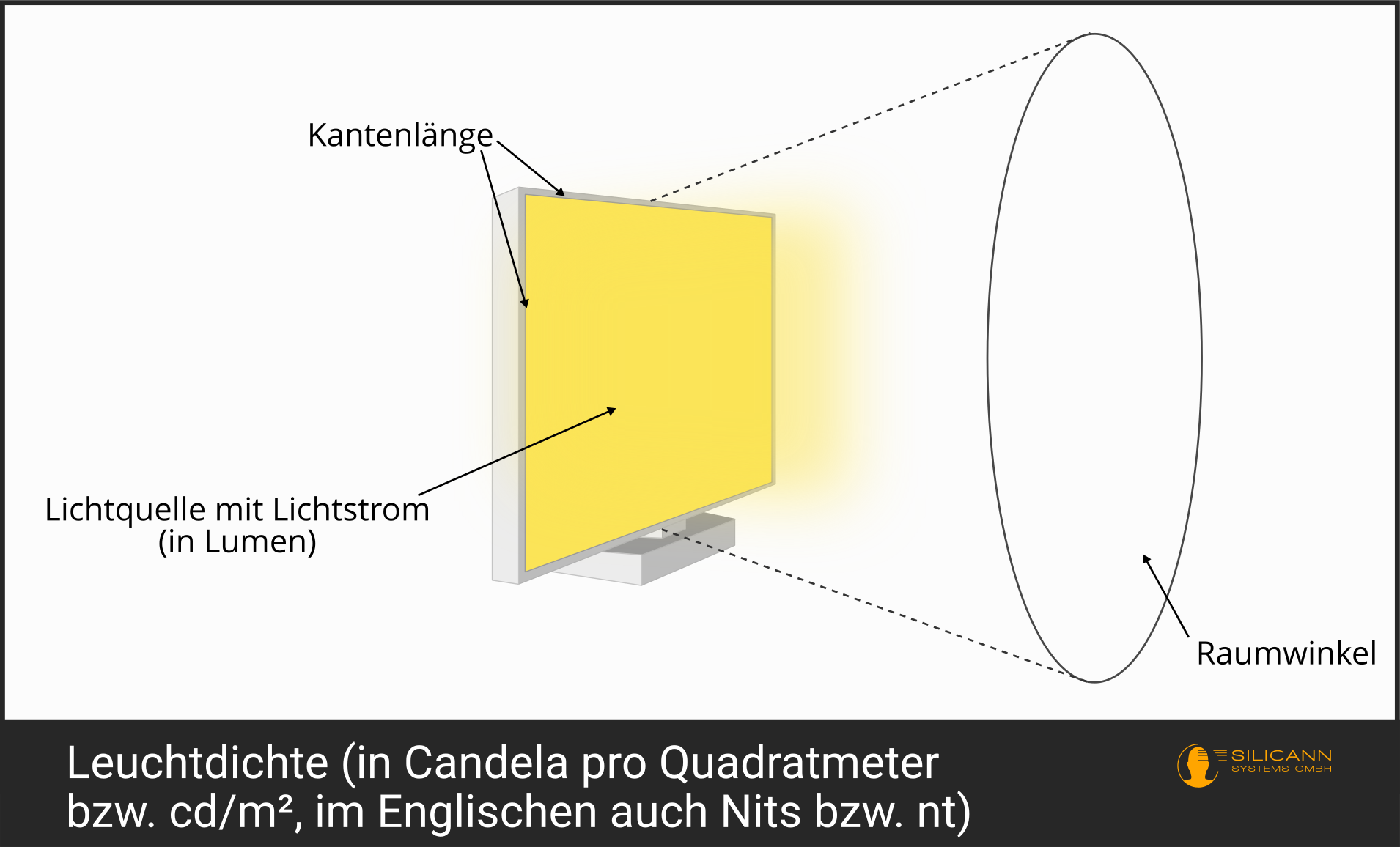
Die Leuchtdichte beschreibt im Kern eine Kombination aus der spezifischen Lichtausstrahlung (also der Fläche der Ausstrahlung) und gleichzeitiger Beachtung des Raumwinkels, innerhalb dessen das Licht ausgestrahlt wird.
Der Raumwinkel kennen wir schon von der Lichtstärke - dort wurde die Quelle des Lichts jedoch vereinfacht als Punkt angenommen. Hier haben wir es also im Grunde mit der Lichtstärke im Verhältnis zur strahlenden Fläche zu tun. Dementsprechend ist die Einheit der Leuchtdichte Candela pro Quadratmeter.
Cd/m² ist die SI-Einheit für die Leuchtdichte und wird praktisch weltweit verwendet. Gelegentlich trifft man jedoch auch auf die Bezeichnung Nits. Sie stammt aus dem englischsprachigen Raum und meint genau dasselbe: 1 nt = 1 cd/m².
Beleuchtungsstärke
Alle bisher angeführten physikalischen Größen dienten der Beschreibung von Lichtquellen. Es gibt jedoch auch Größen, die nicht die Quelle des Lichts, sondern die beleuchtete Fläche betrachten.
Die allgegenwärtige Größe ist hier die Beleuchtungsstärke, vermutlich besser bekannt durch ihre Einheit Lux.
Natürlich behandelt die Beleuchtungsstärke nicht etwas grundsätzlich anderes, sondern verschiebt den Bezugsrahmen nur von der Quelle des Lichts auf dessen Ziel. Deshalb wird die Einheit Lux auch aus Einheiten abgeleitet, die Lichtquellen beschreiben. Und es geht wieder um Beleuchtung, nicht Bestrahlung, d.h. es gibt wieder den Bezug auf das menschliche Sehsystem und die Einschränkung auf sichtbares Licht statt elektromagnetischer Strahlung allgemein.
Definiert wurde 1 Lux vom IEC als die Beleuchtungsstärke, die von einem Lichtstrom in Höhe von 1 Lumen auf einer (gleichmäßig beleuchteten) Fläche von 1 Quadratmeter erzeugt wird: lx = lm/m².
Haben wir statt des Lichtstroms in Lumen die Lichtstärke in Candela, dann können wir auch damit die Beleuchtungsstärke berechnen. Die Lichtstärke erweitert den Lichtstrom ja um den Raumwinkel der Ausstrahlung. Befindet sich die Lichtquelle in einem Meter Abstand und strahlt sie über einen 1 sr breiten Raumwinkel, dann beleuchtet sie wiederum eine Fläche von genau 1 m². 1 Lux ist also auch gleich 1 Candela pro Quadratmeter - allerdings beschreiben die Meter hier den Abstand von Lichtquelle und beleuchteter Fläche, nicht die Fläche selbst!
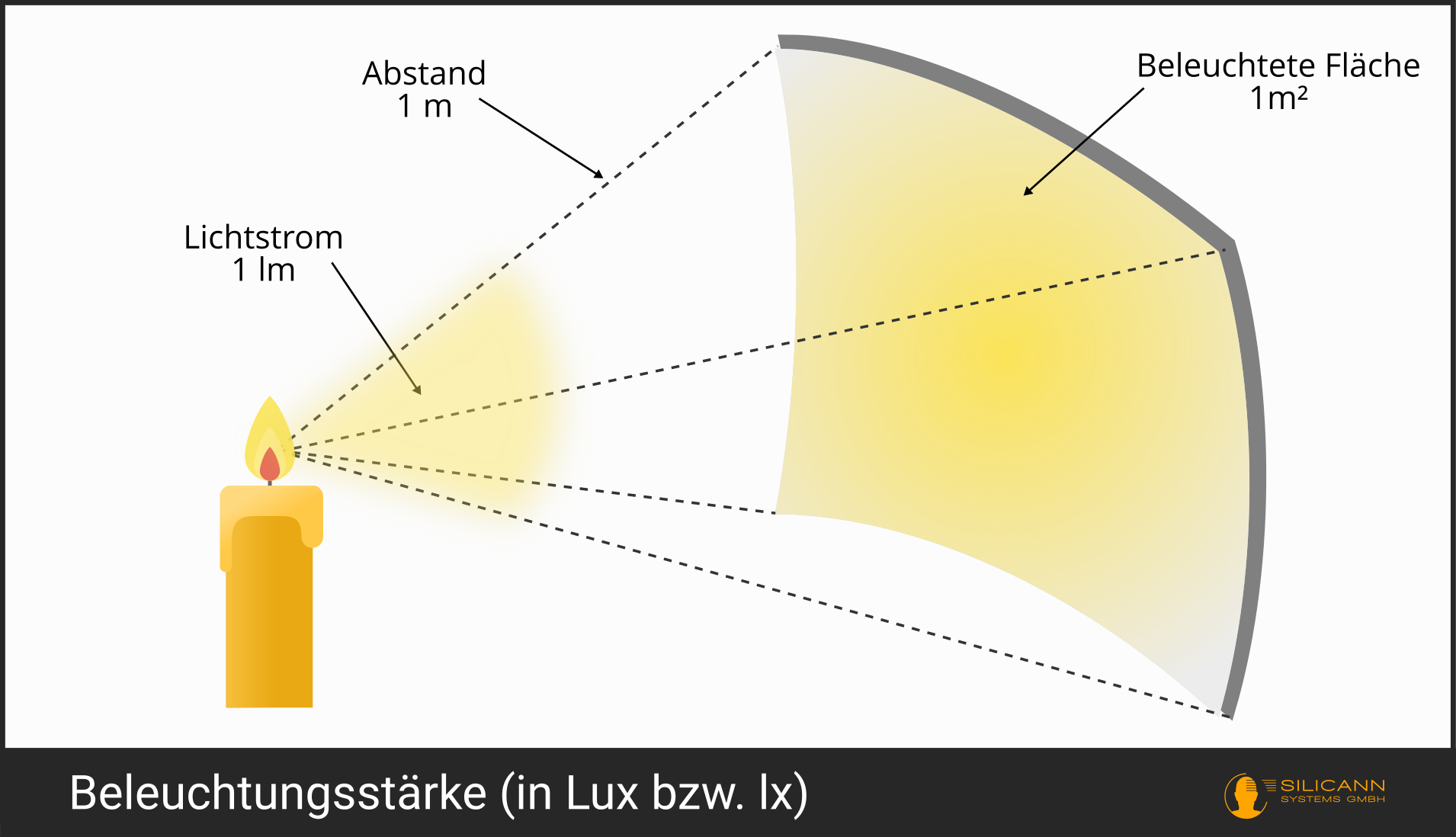
Umrechnen der verschiedenen photometrischen Größen.
Gewappnet mit dem Wissen um die verschiedenen photometrischen Größen können wir nun auch versuchen, Lichtquellen und beleuchtete Flächen miteinander zu vergleichen, auch wenn deren Eigenschaften in jeweils unterschiedlichen Größen angegeben wurden.
Wichtig ist dabei jedoch, dass die Umrechnung auch physikalischen Sinn ergibt - das Vorhandensein der passenden Einheiten reicht hier nicht immer aus.
Spezifische Lichtausstrahlung und Lichtstrom umrechnen
Zwischen diesen beiden Größen umzurechnen ist sicherlich das einfachste Szenario, denn hier müssen wir nur die Fläche des Strahlers kennen. Multiplizieren wir die spezifische Lichtausstrahlung mit der Fläche des Strahlers, dann erhalten wir den Lichtstrom in Lumen.
Lichtstrom und Lichtstärke berechnen
Handelt es sich um einen punktförmigen Strahler und haben wir eine Helligkeitsangabe in Candela, dann müssen wir nur den Raumwinkel der Abstrahlung bestimmen, um den Lichtstrom zu erhalten. Strahlt die Lichtquelle komplett kugelförmig ab, dann beträgt ihr Raumwinkel 4 × π = 12,57 Lumen pro Candela.
Oder andersherum: Eine Glühlampe mit einer Helligkeitsangabe von 400 lm ist gleichwertig zu einer anderen Lichtquelle mit 31,8 cd:
400 lm / (4×π) = 31,8 cd.
Umrechnen von Lichtstärke und Leuchtdichte
Der wesentliche Unterschied zwischen Lichtstärke und Leuchtdichte ist die Größe des Strahlers: Die Lichtstärke nimmt eine punktförmige Lichtquelle an, während die Leuchtdichte genutzt wird, um einen Flächenstrahler zu beschreiben.
Die Unterscheidung gibt es ja eingangs beschrieben nicht grundlos, denn unser Sehsystem nimmt eine Lichtquelle mit geringerer räumlicher Ausbreitung als heller wahr als eine gleich starke Lichtquelle, die jedoch eine größere Fläche hat.
Wenn wir jedoch rein rechnerisch eine Lichtquelle mit Lichtstärke in Candela und eine Lichtquelle mit Leuchtdichte in cd/m² vergleichen wollen, dann müssen wir letztere schlicht mit ihrer Fläche multiplizieren.
Für den subjektiven Helligkeitseindruck wäre das wenig sinnvoll (eine LED mit 300 Candela würde uns viel heller erscheinen als ein Monitor mit 300 cd/m²). Wir könnten jedoch so rechnen, wenn wir z.B. die Frage beantworten wollen, ob die LED und der Monitor denselben Raum ungefähr gleich stark erhellen.
Lichtstrom und Leuchtdichte berechnen
Dieselben Bedenken der Sinnhaftigkeit eines Vergleichs gelten auch bei der Gegenüberstellung von Lichtstrom und Leuchtdichte. Darf der subjektive Helligkeitseindruck ignoriert werden, dann muss der Wert des per Leuchtdichte beschriebenen Strahlers schlicht mit seiner Fläche und 4 × π, dem Raumwinkel einer vollen Kugel, multipliziert werden.
Ein Beispiel: Wir wollen ein 17"-Display mit einer Helligkeitsangabe von 300 cd/m² und eine Glühlampe mit 300 lm vergleichen. Ein 17"-Display im 16:9-Format hat Kantenlängen von ca. 35,5 und 20 cm. Multipliziert mit der Fläche (0,355 × 0,2) erhalten wir eine Lichtstärke von 21,3 cd. Multiplizieren wir jetzt noch mit 4 × π, dann erhalten wir einen Lichtstrom 267,7 lm. Die mit 300 lm angegeben Glühlampe strahlt also insgesamt etwas stärker - ohne Lampenschirm jedoch in alle Richtungen.
Rechnen mit Beleuchtungsstärke und Lichtstärke
Bei der Beleuchtungsstärke wird es etwas interessanter, weil sie im Unterschied zu allen anderen beschriebenen Größen nicht den Strahler, sondern stattdessen die bestrahlte Fläche behandelt. Andererseits verhält sich die beleuchtete Fläche ja wiederum selbst als Strahler, wenn wir das von dort reflektierte Licht betrachten.
In der Praxis wird häufig mit Licht und Beleuchtung gerechnet, wenn etwa durch Normen eine bestimmte Beleuchtungsstärke vorgegeben ist und nun auf dieser Basis die passenden Lichtquellen bestimmt werden müssen.
Wir möchten z.B. einen Arbeitsplatz mit 1000 lx beleuchten. Die Lampe wird in 80 cm Abstand über dem Tisch hängen, und ihre Helligkeit wird als Lichtstärke, also in Candela angegeben. Der Einfachheit halber gehen wir davon aus, dass das Licht der Lampe genau die Fläche des Tisches beleuchtet.
Das rechnerische Verhältnis zwischen den Einheiten lautet Lux = Candela pro Quadratmeter. Wichtig ist hier allerdings, dass es sich bei den Quadratmetern nicht um die beleuchtete Fläche, sondern um das Quadrat des Abstands zur Fläche handelt. Die Lichtstärke in Candela beschreibt ja die Strahlung in einem bestimmten Raumwinkel, und dieser Raumwinkel umfasst in einem Meter Abstand eine Fläche von einem Quadratmeter.
Im Fall unseres beleuchteten Tisches müssen wir also die Beleuchtungsstärke mit dem Quadrat des Abstands der Lampe multiplizieren: 1000 lx × 0,8 m² = 640 cd. Die Lampe muss also eine Lichtstärke von mind. 640 cd haben, um den Tisch mit 1000 lx zu beleuchten.
Beleuchtungsstärke und Lichtstrom umrechnen
Bleiben wir beim Beispiel von eben, ein Arbeitstisch soll mit 1000 Lux beleuchtet werden. Diesmal jedoch gehen wir davon aus, dass die Lampen über ihren Lichtstrom, also in der Einheit Lumen, bestimmt werden.
Auch wenn die Lampe in Lumen angegeben wird, also der Ausstrahlungskegel vom Hersteller unbeachtet bleibt, müssen wir diesen Raumwinkel in der realen Welt mitbedenken. Nehmen wir an, dass die Lampe in diesem Beispiel, von der Seite betrachtet, einen Öffnungswinkel von 90° hat.
Wir können in diesem Fall die Beziehung zwischen Lichtstärke und Lichtstrom nutzen: Lichtstärke ist Lichtstrom geteilt durch den Raumwinkel der Ausstrahlung.
Zunächst rechnen wir also die Lichtstärke in Candela aus und danach multiplizieren wir mit dem Raumwinkel, um den nötigen Lichtstrom zu erhalten.
Die Vorgabe ist eine Beleuchtungsstärke von 1000 Lux, und der Lampenabstand beträgt nach wie vor 80 cm. Damit bleibt auch die Lichtstärke gleich: 640 cd.
Jetzt müssten wir nur noch den Raumwinkel herausrechnen. Das Problem: Wir haben nur die Angabe eines ebenen Winkels, also ein Winkel in der Fläche, nicht im Raum.
Vom ebenen Winkel zum Raumwinkel
Ein Raumwinkel muss keinen Kreiskegel beschreiben, aber wenn er es tut, dann lässt sich verhältnismäßig einfach zwischen Raumwinkel und ebenem Winkel umrechnen.
Zunächst zur grundsätzlichen Sinnhaftigkeit der Rechnerei. Ein Raumwinkel lässt sich ja als Kegel beschreiben, der seinen Ursprung im Mittelpunkt einer Kugel hat und seine Basis auf der Oberfläche der Kugel. Diese Kugel können wir halbieren, so dass wir den Querschnitt des Kegels betrachten, den der Raumwinkel beschreibt. Weil die Fläche, die Basis des Kegels, ein Kreis, also symmetrisch ist, gibt es eine klare Beziehung zwischen diesem 2D-Querschnitt und dem dreidimensionalen Kegel.
Der Raumwinkel errechnet sich aus dem ebenen Winkel (in Radiant, nicht Grad) wie folgt:
Raumwinkel = 2×π×(1-cos(Winkel/2))
Liegt der Flächenwinkel in Grad statt Radiant vor, dann geht es so:
Raumwinkel = 2×π×(1-cos(Winkel×π/360))
Zurück zu unserem beleuchteten Arbeitstisch: Bei einer Lampe mit einem Öffnungswinkel von 90° hat der Raumwinkel des ausstrahlenden Lichts also laut dieser Formel eine Größe von 1,84 sr. Lichtstrom ist gleich Lichtstärke mal Raumwinkel. Die Lichtstärke betrug 640 cd, also haben wir das Ergebnis: Die Lampe muss einen Lichtstrom von 640 cd × 1,84 sr = 1177 lm haben.
Alternativ ist der Ausstrahlungswinkel vielleicht vernachlässigbar, z.B. bei einer Anordnung von LED-Panels an der Zimmerdecke. Dann kann tatsächlich einfach die Formel Lumen = Lux × Quadratmeter angewendet werden. Ein passendes Szenario: Wir wollen in einem Zimmer dieselbe Beleuchtung realisieren, die auch draußen an einem wolkigen Wintertag herrscht, laut Wikipedia ca. 3500 lx. Das fiktive Zimmer hat eine Größe von 30 m². Dann benötigen wir an der Decke Panels mit einem Lichtstrom von sportlichen 3500 × 30 = 105000 lm. Vielleicht kann es im Zimmer doch ein wenig dunkler sein als draußen.
Beleuchtungsstärke und Leuchtdichte berechnen
Auch aus der Leuchtdichte, meist für Displays angewendet, lässt sich die resultierende Beleuchtungsstärke ableiten - und umgekehrt. Das Szenario: Eine Person liegt im dunklen Zimmer in ihrem Bett und nutzt ihr Handy. Wir möchten die Beleuchtungsstärke auf der Fläche des Gesichts berechnen. Es ist ja schon dunkel, darum wurde das Display auf 200 cd/m² heruntergeregelt. Das Display selbst ist 6,5 cm breit und 15 cm hoch und wird in einem Abstand von 40 cm vom Gesicht gehalten.
Zunächst müssen wir mit der tatsächlichen Fläche des Displays multiplizieren, um die Lichtstärke in Candela zu erhalten: 200 × (0,06 × 0,15)² = 1,95 Candela.
Damit haben wir die Fläche des Displays aus der Gleichung genommen und haben nur noch die schon behandelten Umrechnung von Lichtstärke in Beleuchtungsdichte vor uns: Beleuchtungsdichte = Lichtstärke durch Abstand²:
1,95 / 0,4² = 12.2 Lux
Wir können auch hier den Ausstrahlungswinkel nur deshalb ignorieren, weil der Winkel eines Handy-Displays gerade so schmal ist, dass bei der genannten Entfernung praktisch das gesamte Licht auch tatsächlich auf dem Gesicht landet (der lokale Feldversuch zeigte einen ebenen Winkel von ca. 10°, d.h. ca. 0,0024 sr). Würde ein signifikanter Teil des Lichts das Gesicht verfehlen bzw. nur einen Teil des Gesichts bestrahlen, dann müssten wir die Rechnung um den Raumwinkel erweitern.


